Exponential Equations I: Growth and decay
by Anne E. Egger, Ph.D., Janet Shiver, Ph.D., Teri Willard, Ed.D.
Listen to this reading
00:00Did you know that you can use a type of math problem called an exponential equation to figure out how much money you will have in your bank account after collecting interest over a number of years? Scientists also use exponential equations to estimate the age of an object through carbon dating or to predict how quickly a disease is likely to spread through a population. In fact, exponential equations are used in every branch of science.
Exponential equations have a variable as an exponent and take the form y= abx.
The y-values of (or solutions to) an exponential equation follow a geometric progression and are the result of repeated multiplication by the same amount.
The shape of graphs of exponential equations indicate exponential growth or decay.
Exponential growth and decay are both common processes and exponential equations can be used to model and predict in many disciplines.
- exponent
- a small number or symbol high and to the right of a base number that indicates how many times the base number should be multiplied by itself; the power to which the base number is raised. Example: bx, where b is the base number and x is the exponent.
- linear
- in mathematics, an equation that makes a straight line when plotted on a graph.
- variable
- in mathematics, an unknown value, commonly represented by x or y.
St. Matthew Island is a remote island in the Bering Sea off Alaska. In 1944, the United States Coast Guard set up a station on the island to aid planes and ships in navigating the Bering Sea. To provide an emergency food source for the 19 men at the station, 29 reindeer, consisting of 24 females and 5 males, were introduced to the island (Figure 1). A few years later, the Coast Guard abandoned the island, leaving the reindeer behind. In 1957, researcher Dave Klein, a biologist working for U.S. Fish and Wildlife Service, visited the island and counted 1,350 healthy reindeer, whose population had exploded due to the lack of predators and the abundance of lichens, their primary food source. Klein returned to the island in 1963, where he was astounded to find that the population had swelled to over 6,000, which represents an amazing 47 reindeer per square mile.

Three years later in 1966, Klein and others returned to the island to find that the reindeer population had plummeted from 6,000 healthy reindeer to 42 sickly reindeer. Of those 42, 41 were females and 1 was a male that had abnormal antlers, a sign that it was probably unable to reproduce. Overgrazing had wiped out the lichen supply, a significant winter food source for the reindeer. This lack of food caused a 40% decrease in the body weight of the animals and made them less able to withstand the harsh winters of St. Matthew Island (Klein, 1968). By the 1980s, no reindeer remained on the island.
Figure 2 shows Dave Klein’s graph of the reindeer population on St. Matthew Island. Notice that the population of reindeer on the island changed relatively slowly from year to year in the beginning, but as time went on, it increased by larger and larger amounts. This pattern of growth should make intuitive sense: As more reindeer populate the island, more births occur. And so the population increases more rapidly as time goes on, resulting in the curved, concave-up shape of the graph – until 1963, at least.
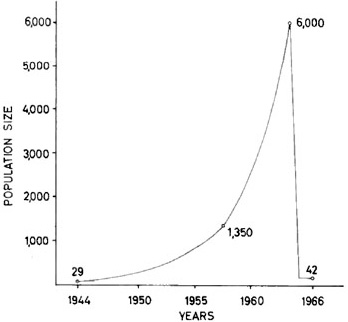
Unlike the slope of a straight line, the slope of the curve on the graph is not constant, so the equation that describes the graph has to have a different form than a linear equation (which is written in the form y = mx + b; see our module on Linear Equations in Science: Relationships with Two Variables for more information). Instead, the equation that describes this shape has a variable as an exponent, such as y = 5x, and thus is called an exponential equation.
The rapid increase in the number of reindeer on St. Matthew Island can be described with an exponential equation, and is called exponential growth. This type of growth (and its opposite, exponential decay) is a common natural phenomenon, and thus exponential equations are frequently used in all branches of science. After describing these kinds of equations in more detail, we will determine the equation that describes the reindeer population growth.
Early history of exponential equations
Some of the earliest records of mathematical problem solving come from ancient Egypt in the form of papyri that were written between 1850 and 1600 BCE. One of these, the Rhind Mathematical Papyrus, is a collection of math problems written around 1650 BCE whose title is “Correct method of reckoning for grasping the meaning of things and knowing everything that is, obscurities…and all secrets,” (see Figure 3 for a picture of the Rhind Papyrus). This was not a purely academic document: The problems in the papyrus were used to manage food supplies for cities, among other things.

One problem asks:
In a certain village, there were 7 houses; each house had 7 cats; each cat caught 7 mice; each mouse would have (were it not for the cats) eaten 7 ears of spelt; each ear of spelt produced 7 hekats of grain at harvest. How many hekats of grain were saved by the presence of the cats? (as quoted in Curtis, 1978).
If we put that information in table form, here is what you get:
| Item | How many? | Exponential notation |
Total number |
|---|---|---|---|
| House | 7 | 71 | 7 |
| Cats | 7 x 7 houses | 72 | 49 |
| Mice | 7 x 7 cats x 7 houses | 73 | 343 |
| Ears of spelt | 7 x 7 mice x 7 cats x 7 houses | 74 | 2401 |
| Hekats | 7 x 7 ears x 7 mice x 7 cats x 7 houses | 75 | 16807 |
The numbers are increasing rapidly by multiplication of the same number by itself in what is called a geometric progression. The Egyptians did not use the symbolic notation of an exponent that we do today, but they were very familiar with the idea of a geometric progression.
Use of the exponential notation came much later, when René Descartes defined the notation a2 as being equivalent to aa, "for multiplying a by itself" and a3 as "for multiplying it yet again by a, and so on to infinity" (Descartes, 1637). At the time, however, Descartes did not use the word "exponent" (exposant in French). In fact, it is not entirely clear when the word "exponent" began to be used to describe the use of the right-hand superscript as a mathematical expression, and most seemed to think it needed no explanation at the time. To address this lack of explanation, Charles Reyneau published Analyse demontrée in 1708, in which he states, "The only calculation that is not explained in the Theories of Algebra must be spoken of, and this is exponents or powers" (Cajori, 1913). By the early 1700s, therefore, both the mathematical concept of exponential equations and the notation of exponents were firmly established.
Comprehension Checkpoint
What are exponential equations?
An exponential equation is an equation in which a variable occurs in the exponent. For example, y = 5x is an exponential equation since the exponent is the variable x (also said as "5 to the power of x"), while y = x5 is not an exponential equation since the exponent is 5 and not a variable. We often write exponential equations as y = abx, where a and b are constants (numbers that don't change value) and x and y are variables. In addition, a is called the initial value, and b is called the base value. As in most areas of math and science, x is considered the independent or manipulated variable, and y is the dependent or response variable, because the value we get for y depends on what we substitute in for x.
In exponential equations, the value of b, the base value, has some restrictions. The constant b cannot be equal to 1 and it must be greater than 0. Why? If b = 1, then no matter what the value of x is, the value of y is always the same number a; if b = 0, then the value of y is always 0. When we graph the equation with these values we would get a horizontal line (thus a linear equation) instead of an exponential curve. If b < 0, some values of x will result in values of y that are not real. For example, if x is a fraction like ½ and b = -2, then (-2)½ = √-2, which is not a real number and cannot be graphed on a real number axis.
Graphing an exponential equation
Let’s look at the behavior of an exponential equation, y = 5x, and compare it to a linear equation, y = 5x + 1. To see the differences, we will graph both equations by first completing a table of values, shown below.
| Linear equation | |||
|---|---|---|---|
| x | y = 5x + 1 | y | Change in y-value |
| -1 | 5(-1)+1 | -4 | n/a |
| 0 | 5(0)+1 | 1 | +5 ("plus 5") |
| 1 | 5(1)+1 | 6 | +5 |
| 2 | 5(2)+1 | 11 | +5 |
| 3 | 5(3)+1 | 16 | +5 |
| Exponential equation | |||
|---|---|---|---|
| x | y = 5x | y | Change in y-value |
| -1 | 5-1 | 1/5 | n/a |
| 0 | 50 | 1 | x5 ("times 5") |
| 1 | 51 | 5 | x5 |
| 2 | 52 | 25 | x5 |
| 3 | 53 | 125 | x5 |
The y-values of a linear equation are the result of simply adding the same value over and over again (in this case, 5), called an arithmetic progression. In contrast, the y-values of an exponential equation are the result of repeated multiplication by the same amount (again, 5), called a geometric progression. We can compare these two sets of results graphically, shown in the graph in Figure 4.
Figure 4: Graph of the linear equation y=5x+1 (red line) compared to the graph of the exponential equation y=5x (blue line).
The graph of the linear equation is a straight line and increases at a steady or constant rate. The graph of the exponential equation, on the other hand, is not a straight line, and increases at an increasing rate, forming a curve. Since the powers in an exponential expression indicate the number of times the base number is to multiply itself, such as 23 = 2 * 2 * 2, then as the powers increase, we are multiplying by the same value more and more times. This relationship causes y to increase slowly at first and then more rapidly as the x values increase, which causes the graph to appear curved or concave in shape.
The graph of an exponential equation when the initial value, a, is positive can be classified as either exponential growth (increasing to the right) or exponential decay (decreasing to the right) depending on the value of b; see the two graphs in Figure 5 to compare growth and decay.
Figure 5: Two graphs comparing exponential growth and decay.
Exponential growth occurs when b > 1, and y-values increase to the right. Exponential decay occurs when 0 < b < 1, and y-values decrease to the right. Both graphs are concave-up.
When a < 0, the graphs of exponential equations become concave down, and increasing x-values yield increasingly negative y-values. While this is perfectly acceptable mathematically, it is rare in science that the initial value a would be negative. Thus, the majority of graphs we use in science look like either exponential growth or decay curves shown in Figure 5.
Comprehension Checkpoint
Sample problem 1
Suppose you are a 2015 college graduate and are offered a job as an ecologist at a starting salary of $40,000 per year. To strengthen the offer, the company promises you annual raises of 5% per year for at least the first five years of work. Let’s examine how your salary will change over a five-year period.
Let x = the number of years since the beginning of your contract and let y = the annual salary (in $) after x years. A raise results in 100% (original amount) + 5% (raise) = 105%, or 1.05, multiplied by your previous salary. (Keep in mind that you must express the percent as a decimal.) The results of these calculations are shown in the table below.
| x Years | Salary Calculation with 5% Raise | Yearly Salary After Raise |
|---|---|---|
| 0 | 40,000.00 = 40,000.00⋅(1.05)0 | $40,000.00 |
| 1 | 40,000.00 (1.05) = 40,000.00⋅(1.05)1 | $42,000.00 |
| 2 | [40,000.00(1.05)](1.05) = 40,000.00⋅(1.05)2 | $44,100.00 |
| 3 | [40,000.00(1.05)2](1.05) = 40,000.00⋅(1.05)3 | $46,305.00 |
| 4 | [40,000.00(1.05)3](1.05) = 40,000.00⋅(1.05)4 | $48,620.25 |
| 5 | [40,000.00(1.05)4](1.05) = 40,000.00⋅(1.05)5 | $51,051.26 |
Notice that in year 0, representing the initial year of the job, there will be no multiplier to determine the salary, or you could think $40,000.00 • (1.05)0 = $40,000.00 • 1 = $40,000. Then for year 1, $40,000 is multiplied by (1.05)1, or just 1.05. For year 2, $40,000 is multiplied by (1.05) twice, once to get the increase for the first year and a second time to get the additional increase for year 2. This gives us $40,000.00 • (1.05)2. The pattern continues for each additional year with the exponent for 1.05 being the same as the year number, x.
In the salary scenario, the beginning salary is a, the initial value. The value b = (1 + 0.05) or 1.05, which can be thought of as 100% of the previous year’s salary plus a 5% increase. Substituting in both values, the equation becomes y = 40000(1.05)x, where x is the number of years since being hired. This exponential equation allows us to find your salary after any number of years on the job, as long as nothing else changes.
Comprehension Checkpoint
Sample problem 2
Let’s return to the reindeer on St. Matthew Island and write an exponential equation to represent their population growth. Because we don't have data every year or at regular time intervals, this problem requires a little bit more manipulation to solve. First, we need to convert the year (such as 1957) to the years since reindeer were introduced, or years since 1944. The number of years since reindeer were introduced is x in this equation, and y is the number of reindeer on the island. We have three data points to work with: 1944, or 0 years after introduction; 1957, 13 years after introduction, and 1963, 19 years after introduction (see the table below).
| Year | Years since introduction (Year – 1944) |
Number of reindeer |
|---|---|---|
| 1944 | 0 | 29 |
| 1957 | 13 | 1350 |
| 1963 | 19 | 6000 |
The initial number of reindeer on the island was 29, so a = 29. We need to determine what b is to write the complete equation, but we don’t have regularly spaced time intervals to determine this easily by hand. With a graphing calculator or spreadsheet program, you can enter the ordered pairs in the table above ((0, 29), (13, 1350), and (19, 6000)) into the list function and find an exponential equation for the data set. An equation generated through this statistical process, called regression, is y = 30.14(1.33)x, and the value of b is determined to be 1.33. Compare this with the value of b from sample problem 1, 1.05, where the growth rate of the salary was 5% per year. Using the same logic (1.33 – 1.00 = 0.33 or 33%), the equation we derived suggests a 33% growth rate in the reindeer population per year!
This equation can be used to approximate the number of reindeer on the island during any year from 1944 to 1963. However, we need to remember that this is a mathematical model derived from limited data and the actual data may be slightly different from the values generated by the exponential equation. For example, if we want to predict the number of reindeer on the island in 1963, we can substitute 19 (given that 1963 – 1944 = 19) for the exponent x.
But this value is higher than the actual number of reindeer counted on the island at this time. The difference between the number of reindeer counted and the mathematical prediction could be due to a number of factors, including counting errors by the researchers, natural variability in the reindeer population, and an imprecise mathematical model, which could be the result of having only three data points to work with (for more information on mathematical models, see our module Modeling in Scientific Research).
Exponential equations in science
Exponential equations are applied in a wide variety of situations in science, from modeling the spread of a viral disease in a population to estimating the atmospheric pressure at a given altitude to chain reactions in nuclear fission. All of these processes involve a geometric progression: One person with a virus can infect ten others, for example, and each of those ten people can infect ten more. In all of these cases, real-world data can be modeled using exponential equations, and these equations can provide predictions of future behavior. Solving exponential equations is a valuable tool for finding variables such as growth rate, decay rate, the amount of time that has passed, or an amount of something at a given time.
Table of Contents
Activate glossary term highlighting to easily identify key terms within the module. Once highlighted, you can click on these terms to view their definitions.
Activate NGSS annotations to easily identify NGSS standards within the module. Once highlighted, you can click on them to view these standards.